CaCO3
dispersion in polymer flow:
experimental study and simulation of rupture during twin screw extrusion.
D.
Hochereau (a,b) , P. Descamps (a), P. Leempoel (a) , D. Dochan (b)
(a) Dow Corning Coordination Center,
Parc Industriel,B7180 Seneffe
(b) Cesame, Université Catholique de Louvain,
av, G.Lemaître, 4, B1348 Louvain La Neuve, Belgium.
Contact
: Dominique Hochereau
Abstract
We studied the behavior of precipitated calcium carbonate (CaCO3) filler in silicone polymer flow during twin-screw extrusion and laboratory simulation. A simplified model considering sphere doublets in flow field is used to predict the dispersion of agglomerates. The calculations are compared to filler breakage achieved with a laboratory experiment and also to samples collected from twin-screw extrusion. Particle size distributions (PSD) are determined using a laser diffractometer and agglomerate evolution is observed with optical microscope. The observed PSD evolutions in both cases are very consistent with the model hypothesis. We found that agglomerates break in fragment of similar size, which is in good agreement with the sphere doublet model. We show that the model for PSD evolution can be adapted using a single parameter that is linked to saturation in the rupture mechanism.
1. Introduction
Understanding filler mixing in polymer flow is of fundamental and industrial interest. Though extremely common in the industry, the dispersion of solid powders in polymer is up to now not well understood on a theoretical basis. In this work, we aimed at combining model hypothesis and experimental data in order to highlight some of the process properties. We are focusing on the rupture mechanism and chose to study the dispersion of precipitated calcium carbonate (CaCO3) in silicone polymer matrix.
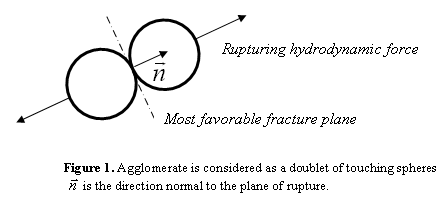
2. A model for rupture: the sphere doublet model
Model for mixing agglomerates in polymer flow consider mainly rupture
and erosion mechanisms. Rupture is characterized by an abrupt splitting
of the agglomerate into a small number of large fragments and tends to
occur at relatively high shear stresses. Erosion, which initiates at lower
shear stresses, is characterized by the continuous detachment of small
fragments from the outer shell of the pellet.(1-3).
We have considered the model of rupture developed by Manas-Zloczower et
al. The agglomerate is considered as a doublet of touching spheres of
equal sizes. This description introduces a single possible rupture plane
between the spheres and an orientation of the doublet. The fracture plane
is the tangent plane to both spheres and rupture can only occur if the
projection of hydrodynamic force orthogonal to the fracture plane exceeds
the binding forces of the spheres. Use of this model requires the construction
of two sub-models: a model for cohesion and a model for hydrodynamic interaction
(1,2). It is shown that this model is actually independent of the size
of the agglomerate and that only particles with a favourable orientation
can break at a given time. The kinetics of rupture is linked to the nature
of the applied flow field. We will here only consider some simplified
hypothesis linked to this approach. We will in particular retain that:
• Any agglomerate breaks into two equal size fragments.
• The mechanism is independent of the size of the agglomerate
• Some agglomerates can not break in the process
These hypotheses allow for multiple fragments rupture because generated fragments can also break in chain. We also expect that agglomerates will stop breaking when their size is too small and is comparable to the aggregate size.
3- Experimental
Experiments for dispersion of CaCO3 filler have been conducted in 2 different ways in order to determine the general behavior. The precipitated CaCO3 powder was Socal powder provided by Solvay and the matrix we used consisted of Dow Corning high viscosity silicone polymer.
The first experiment was carried out using a large industrial Twin Screw
Extruder. The mixer was fed with high viscosity polymer (50000 cs) and
a proportion of CaCO3 filler of 50% of the total weight. The mixer was
set to work at a low throughput of 800kg/h and some samples were collected
for analysis at several positions along the screw axis. these were collected
right at filler incorporation (S1), to set a reference for mixing evolution,
and at the output of the screw (S4). Additional samples were taken from
position at one fourth (S2) and half (S3) of the total length.
Another sample was submitted to a laboratory high-speed mixer consisting
of a rotor included in a cylinder. The 1cm diameter rotor was set at a
speed of 12500 rpm with a distance from the rotor to the cylinder wall
of 1mm. Holes in the cylinder allowed product to flow in and out of the
high shear zone. The sample for this experiment consisted of an incorporation
of about 20% in weight of Socal in a 12500cs silicone polymer. This experiment
was carried out in order to submit the filler to a stress comparable in
terms of time and magnitude to the stress applied to the product in the
extruder. Final product was then collected for analysis.
All samples were analyzed using a laser diffractometer (Malvern Mastersizer X) to determine their particle size distributions (PSD). The device can be fitted with different lenses according to the desired range of sizes to be analyzed. We focused on sizes ranging from 0.1µm to 100µm because it appeared that the evolution due to mixing was mainly taking place in this range. The obtained PSD consists of 32 size channels on a logarithmic scale from 0.1 to 100µm.
4- Experimental results and simulations
The experimental data allow to visualize the product evolution from an initial PSD right at incorporation to a final PSD from samples taken at various stages of the mixing process. We set up a simulation using the simplified hypothesis described above. Starting from an initial size distribution defining a set of particles, we stress that these initial particles, or the created fragments, can break into two equal-sized fragments or remain unbroken until the end of the simulation. Knowing the final distribution, we can then calculate the exact proportion of initial particles and fragments that must remain unbroken in every size class to fit the evolution from a given initial PSD. An illustration of this is given in the figures below, along with the experimental results.
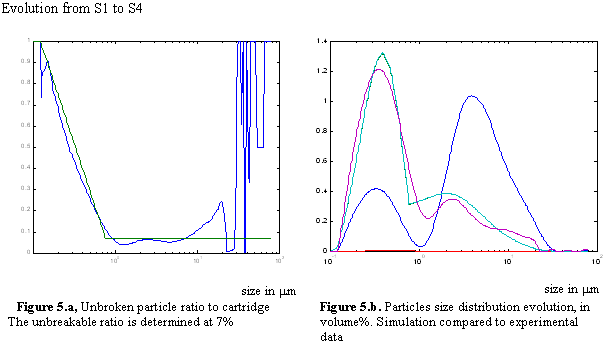
We have reported in figure 2 the PSD evolution for twin-screw extrusion samples (S1, S2, S3, S4). We note that due to the limited range analyzed at once in the diffractometer, our observation does not show the actual distribution of particles below 0.1µm. As a consequence, the PSD may be somehow distorted for smaller size particles. This is however not a limitation for our study as we focus on evolution of larger sized particles, from 1 to 100 µm
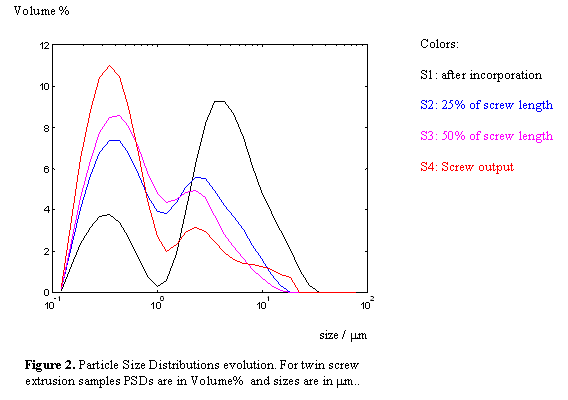
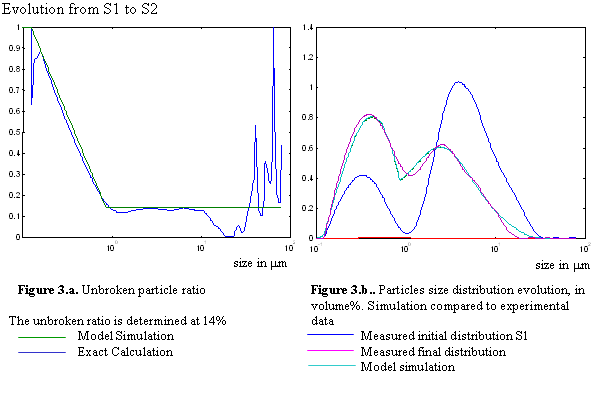
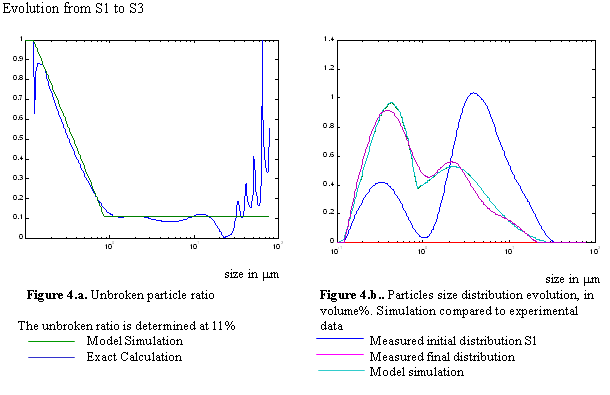
Using the data from S1 as initial distribution, we have calculated the proportions of particles that should remain unbroken for every size class to fit for the evolution. The results are detailed in figures 3, 4 and 5 for samples S2, S3 and S4. On figure 3.b we have reported the initial (blue) and final (magenta) PSD. Then in figure 3.a. we show the exact calculation (blue) of the ratio of particles that should not break to fit the evolution. We notice that this proportion is nearly flat for sizes ranging from about 0.5µm to more than 10µm. We also see that for smaller particle this ratio rapidly grows to 1, which is consistent with the fact that smaller fragments stop breaking when they reach the final aggregate size. It also shows that rupture hypothesis made are very meaningful. These observations allow setting up a predictive simulation considering a size independent ratio for unbroken particles. A simplified distribution for this ratio can be estimated with a constant level for larger agglomerate, keeping the fact that small aggregates do not break. The simplest simulation comes to the determination of two straight lines on the semi-log plot for unbroken ratio (green plot in figure 3.a). The result of the simulation is shown along with experimental data on figure 3.b. (cyan). The calculation is also done for sample S3 and S4, in figure 4 and 5. The percentage of particles that remain unbroken, for the best fitting simulation, is determined to be 14% for S2, 11% for S3 and 7% for S4. We note that these observations are very consistent with the “Manas-Zloczower model” (1,2) for the size-independent mechanisms.
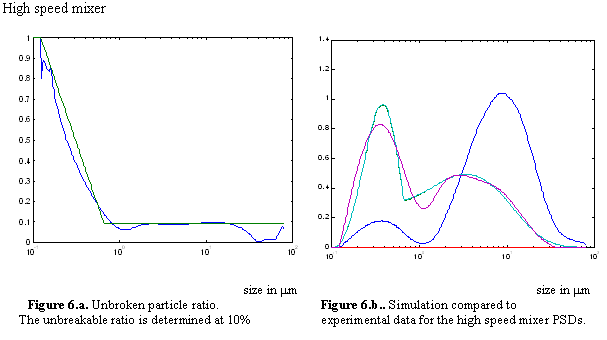
The same calculations and simulation were applied to the laboratory sample,
which underwent breakage through the high-speed mixer. The results are
shown in figure 6. Compared to the extrusion samples data, the results
show a very similar behavior and we can also state here that the model
of rupture also fits very well this case and that the mechanism is shown
to be independent of the particle size, for sizes above the aggregate
size.
5- Conclusions
These first results in our experimental study tend to confirm the behavior
predicted by the Manas-Zloczower model. We first showed that the observed
size distribution evolutions were fully compatible with the hypothesis
considering mainly rupture of particles in equal sized fragments. This
seems to rule out, in this case, the presence of erosion mechanisms. This
is understood because the stresses applied to the samples in both experiments
are believed to be much higher than the cohesion strength of the agglomerate.
Both experiments, in the screw or in the mixer, also let the product flow
for a very short time in the very high shear stress regions. This means
that the chain breakage sequences occur in a very short time in the overall
process. In the case of the screw it is probable that the probability
of a particle to enter several time a high shear region is kept relatively
low.
Our simplified model and simulations appears to be a very interesting
tool to predict mixing evolution during extrusion process. The advancement
of mixing can be characterized all along the screw using a single parameter
that, in simulations, corresponds to the ratio of unbroken particles.
Further experiments are now conducted to help quantify the observed breakage
of these samples. Shear flow simulations will be conducted using a cone
and plate instrument to follow PSD evolution with very well defined applied
stresses and times of application.
Support for this work was provided by Dow Corning and the Wallonia region
(Belgium) in the framework of a first entreprise agreement.
6- References
1. I. Manas-Zloczower, D.L. Feke, Analysis of Rupture in Linear Flow
Fields, Intern. Polym. Processing IV, 1, p3,(1989).
2 I. Manas-Zloczower, Z. Tadmor, Mixing and Compounding of Polymers: theory
and practice, Carl HANSER Verlag, (1994).
3. S.P. Rwei, I. Manas-Zloczower, Characterization of Agglomerate Dispersion
by Erosion in Simple Shear Flows, Polym. Eng. Sc., 31-8, p558, (1991).
4. Z. TADMOR, C.G. GOGOS, Principles of Polymer processing, Wiley, (1979).