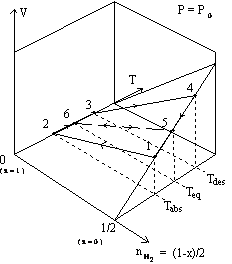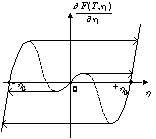Chapitre I :     Transition de phase et hystérésis.

 

Dans ce chapitre, nous abordons l’aspect thermodynamique de l’hystérésis associée à des transformations de phase de premier ordre dans les systèmes métal-hydrogène.

 

1. Introduction                                                                                                                          

2. Transformations de phase                                                                                                   

2.1. RAPPELS THERMODYNAMIQUES                                                                    

2.2. TRANSFORMATION DE PHASE : DÉFINITION                                                

2.3. ORDRE D’UNE TRANSITION : CLASSIFICATION                                           

2.4. LES RAISONS THERMODYNAMIQUES D’UNE TRANSITION DE PHASE   

2.5. TRANSITION DE PHASE DUE AUX INTERACTIONS ÉLASTIQUES : SYSTÈME MÉTAL - HYDROGÈNE                                                                                                       

2.6. EXTENSION DE LA THÉORIE DE LANDAU AUX TRANSITIONS DE PREMIER ORDRE         

3. L’hystérésis                                                                                                                          

3.1. DÉFINITIONS                                                                                                        

3.2. OBSERVATIONS EXPÉRIMENTALES - CLASSIFICATION                            

3.2.1. L’hystérésis de pression                                                                            

3.2.2. L’hystérésis de solubilité / précipitation                                                   

3.2.3. L’hystérésis thermique                                                                             

3.2.4. Hystérésis à composition constante                                                         

3.2.5. Influence de la microstructure                                                                 

3.3. THERMODYNAMIQUE DE L’HYSTÉRÉSIS                                                       

3.3.1. Hystérésis et production d’entropie                                                         

3.3.2. Production d’entropie, cas isotherme                                                      

3.3.3. Production d’entropie, cas isobare                                                          

4. Conclusion                                                                                                                            

Annexe A : Hystérésis et potentiel non-convexe                                                                   

Références                                                                                                                               

1.    Introduction

L’hystérésis est un phénomène abondamment rencontré dans la science des matériaux. Elle se manifeste dans les transformations de phase ou les changements de structure, ou encore dans certaines transitions d’ordre - désordre, sans oublier de mentionner l’hystérésis mise en évidence dans les milieux magnétiques.

            Nous consacrerons notre analyse à la réactivité de l’état solide et en particulier, à l’hystérésis qui se manifeste dans les changements de phase, entre phases solides et phase gazeuse. Bien que ce phénomène ait été depuis longtemps reconnu et identifié, l’étude de l’hystérésis n’a pas toujours été des plus approfondie. Ceci est d’autant plus surprenant que la présence d’hystérésis, dans certains cas, a limité l’exploitation de matériaux à des fins industrielles. C’est le cas des hydrures destinés au stockage ou aux machines chimiques. Les raisons de ce manque d’intérêt peuvent s’expliquer par les difficultés de mise en oeuvre expérimentale qui impliquent le développement de techniques rigoureuses [1].

            Si nous limitons notre approche à la chimie du solide, l’hystérésis est également présente dans les réactions impliquant l’oxygène et la formation d’oxydes  [2][3][4]. On peut citer, par exemple, les oxydes de terres rares ou les oxydes supraconducteurs à haute température critique. L’adsorption de gaz dans les matériaux poreux met également en évidence différents régimes d’adsorption où l’hystérésis se manifeste [5][6].

            L’hystérésis pénalise l’utilisation des hydrures. Ainsi, dans les machines thermiques, l’irréversibilité se traduit par une perte d’énergie dissipée au cours du cycle de formation - décomposition de l’hydrure, alors que dans les batteries à hydrure [7][8][9], la présence d’hystérésis impose une tension de charge plus élevée que la tension de décharge. Le développement d’alliages multiconstituants a permis de limiter cet effet [10][11]. Dans la limite de plusieurs centaines de cycles de charge/décharge, critère imposé par les constructeurs, ces matériaux donnent entière satisfaction. L’hystérésis contribue également au vieillissement accéléré du composé. Pour les composés utilisés dans les batteries, ce problème technique a été partiellement résolu par des modifications d’ordre chimique du composé. Cette solution étant possible dès lors que la plage d’utilisation en température du matériau est bien définie.

            Dans les réactions du type solide - gaz, l’observation macroscopique du phénomène s’effectue par les variables thermodynamiques pression et température. Le point crucial pour tout matériau consiste à corréler l’évolution des propriétés thermodynamiques à l’évolution de la microstructure. En ce qui concerne les hydrures, la tâche se complique car de nombreuses difficultés apparaissent. En effet, les composés intermétalliques sont très sensibles à la contamination par des impuretés gazeuses, en particulier l’oxygène [13][14][15][16][17]. Le composé hydruré devient de plus pyrophorique. Les observations microstructurales, par exemple au MEB ou au MET, demanderont des techniques de préparation des échantillons très spécifiques [18][19][20].

            La thermodynamique reste donc un outil privilégié pour rendre compte du phénomène. Par l’intermédiaire des variables pression, température et composition, il est possible d’analyser l’évolution de ces systèmes au cours des transformations. Expérimentalement, cela revient à cerner et préciser les paramètres sensibles de la transformation afin de fixer les domaines d’existence, les seuils de stabilité ou d’instabilité. Enfin, toutes ces informations doivent permettre d’expliquer la dynamique de la réaction ou de la transformation pour aboutir à l’élaboration contrôlée du matériau hydruré. Ce type de recherches contribue également à préciser la topologie du diagramme de phases pour le domaine de température étudié.

            Après quelques rappels de thermodynamique (2.1) , nous définissons les transformations de phase (2.2.) et les propriétés importantes qui y sont associées (2.3. et 2.4.). Puis nous abordons des notions spécifiques aux systèmes MH (2.5.). Nous faisons ensuite un rappel de la théorie de Landau permettant de faire le lien entre transition de phase et hystérésis (2.6.). Dans la partie suivante (3.), nous proposons une revue des outils thermodynamiques adaptés à la caractérisation de l’hystérésis. Après quelques définitions (3.1.), nous abordons au cas par cas l’observation expérimentale du phénomène (3.2.) puis un calcul de l’entropie produite associée à des phénomènes cycliques (3.3.).

2.    Transformations de phase

2.1.       rappels THermodynamiques

Une phase est constitutive d’un système. Elle se distingue physiquement par son état : gaz, liquide ou solide. Elle est homogène à l’échelle macroscopique pour une composition constante. Enfin, une phase peut être séparée du reste du système, ce qui revient à dire que les grandeurs extensives varient de manière continue à l’intérieur de la phase, tandis que des discontinuités seront présentes aux limites de phase.

            Dans ces conditions, si les critères de stabilité de l’équilibre thermique sont satisfaits, la phase reste stable et homogène, et possède des propriétés propres à cet état.

 

            Se référant à la fonction de Gibbs, G(T,P,ni), fonction d’ordre zéro de la thermochimie dont les variables se divisent en grandeurs intensives (T,P) et extensives (ni), nous allons pouvoir envisager l’évolution du système par rapport à l’équilibre, à composition constante, et fixer les conditions d’apparition et de disparition d’une phase. Conservant une vision mathématique du phénomène, on voit immédiatement que les conditions de stabilité sont régies par les grandeurs issues des dérivées premières et secondes de la fonction G, définie et continue.

            Les dérivées partielles du premier ordre de G par rapport aux variables intensives sont au nombre de deux :

                                                                                           (1)

Il y a trois dérivées partielles au second ordre de la fonction G :

                                                                         (2)

Remarquons que, bien que suffisantes, les expressions ci-dessus ont évolué avec l’usage, donnant lieu à de nouvelles définitions. Citons, pour la thermochimie :

                                                                           (3)

En rappelant que quatre grandeurs du second ordre s’expriment à partir des trois autres, cette propriété est illustrée par les relations suivantes :

                                                                           (4)

2.2.       transformation de phasE : Définition

On appelle transformation de phase (ou transition de phase) la formation (disparition), au sein d’un système, d’au moins une phase et la disparition (formation) d’au moins une autre phase.

            Ces transformations peuvent être provoquées soit par les variations des paramètres intensifs (T,P,µi) que l’on impose au système, soit à partir des grandeurs extensives (S,V,ni), par échange avec le milieu extérieur. Généralement, ces variations s’accompagnent de diagrammes représentant la fonction G en fonction des paramètres sélectionnés. Le tout étant complété par des projections sur des plans particuliers, par exemple (P,V), (P,T), (V,T) ou bien (P, composition), (T, densité), de diagrammes indiquant l’existence d’une ou plusieurs phases. Prenons pour exemple le diagramme de phases solide/liquide/gaz de la figure 1, représentant un système à un seul constituant; le lien avec les systèmes M-H sera explicité en 2.5.

Figure 1. Diagrammes de phases pour un système à un seul constituant.

a. représentation (P,T)

b. représentation (r,T).

Lorsque le système est dans l’une des régions notée G, L ou S, la variance est égale à 2. En x, le système sera en équilibre stable pour les variables sélectionnées (T,P) ou (T,r). Sur une ligne continue, point y, on observe la coexistence de deux phases. Si la température est abaissée, le système franchit la ligne et subit une transition de phase pour atteindre le point z, nouvel état d’équilibre. On remarque que le système passe, pour certaines conditions, de manière continue de l’état G à l’état L, au delà du point C, sans traverser la ligne de coexistence. Enfin, les trois états peuvent coexister au point triple (T), le système est bloqué à (T,P) ou (T,r). Cela se traduit par une variance nulle. Les potentiels, GL GS et GG sont égaux en ce point.

2.3.       Ordre d’une transition : Classification

En se référant au paragraphe précédent, ainsi qu’aux expressions des dérivées partielles (1) et (2), on voit émerger deux types de transitions suivant que l’on franchit ou non la ligne de coexistence des phases. Dans le premier cas, le franchissement s’accompagne d’une chaleur de transition (l’enthalpie de vaporisation, par exemple), et donc d’une discontinuité dans la dérivée partielle du premier ordre de la fonction G. Au delà du point C, par contre, cette dérivée est continue.

 

            L’analogie entre l’ordre des dérivées partielles et l’ordre de la transition fut introduite par Ehrenfest en 1933. Cette approche permet de généraliser l’ordre d’une transition en analysant le comportement des dérivées de G. Une transition d’ordre n apparaîtra seulement s’il y a des discontinuités dans les dérivées partielles d’ordre n, et supérieur, de G, par rapport aux variables T et P. Pour revenir à notre exemple de la figure 1, la transition indiquée par le chemin xyz est du premier ordre, car on observe une discontinuité du volume (de la densité) et l’existence d’une enthalpie de transformation :

                                       ou encore 

Au point C, température critique, G et les dérivées d’ordre 1 de G sont continues, alors que les dérivées d’ordre 2 par rapport à T et P présentent des singularités ou s’annulent. Nous sommes en présence d’une transition du second ordre. Les équations (3a) et (3c) se réécrivent:

                                                                             (5)

Au point critique, ces grandeurs divergent. L’ensemble de la discussion est résumé sur la figure 2.

Figure 2a. : transition de phase du 1er ordre.

Figure 2b. : transition de phase du 2ème ordre.

            Bien que les transitions du second ordre soient bien moins nombreuses que les transitions du premier ordre, elles ont été sujettes à de nombreux travaux théoriques et expérimentaux [21][35], en particulier, pour comprendre les phénomènes associés au point critique. Notons qu’aujourd’hui ces phénomènes restent encore mieux compris que les transitions du premier ordre. Il est bien établi maintenant que les divergences de  et  à TC sont associées aux divergences de la fonction de corrélation dues aux fluctuations du paramètre d’ordre, paramètre introduit par Landau en 1937 [22].

 

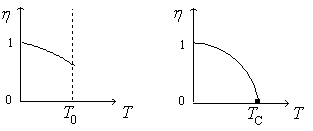
            Jusqu’à présent, nous nous sommes contentés d’une description ‘macroscopique’ de la transition, résultant essentiellement d’observations expérimentales. Abordons maintenant l’aspect structural et microscopique. En se maintenant à une température inférieure à TC , mais au dessus du point triple, pour la transition G-L, on constate que les différences notables des propriétés se retrouvent dans la différence des densités, mais également au niveau de l’environnement moléculaire moyen. Le système biphasé gaz - liquide possède dans chaque phase une structure locale de symétrie sphérique. A TC , les densités sont égales et la symétrie est conservée. Par contre, l’environnement se modifie si l’on considère la transition liquide - solide cristallin. On peut imaginer un liquide et un cristal de même densité, mais même dans cette hypothèse, localement, les différences de symétrie subsistent dans le liquide et dans le solide. Dans ces conditions, il n’y aura pas de température critique. On voit donc apparaître l’importance des conditions de symétrie dans la détermination de l’ordre d’une transition. Une propriété de symétrie existe ou n’existe pas, elle ne peut pas être partiellement présente. C’est le point de départ de la théorie de Landau qui observe que, dans la plupart des cas, la phase ordonnée possède une symétrie plus basse en comparaison de la phase désordonnée. Dans le langage actuel, on parle de brisure de symétrie, que l’on met en valeur par le paramètre d’ordre, non nul dans la phase de plus basse symétrie ou ordonnée, nul pour des températures au dessus de la température de transition. Soit h ce paramètre, la situation est schématisée sur la figure 3.

Figure 3a. : transition du 1er ordre

Figure 3b. : transition du 2ème ordre.

 

La théorie de Landau a servi de base à de nombreux développements où l’on s’est attaché à résoudre ce caractère d’universalité que traduisent les courbes représentant la variation du paramètre d’ordre au voisinage de TC. L’ultime développement a conduit à la théorie de Wilson [23], qui permet de tenir compte des fluctuations du paramètre d’ordre (et donc de la composition) non prises en considération dans le modèle de Landau. Il apparaît que tous les exposants critiques sont susceptibles d’être calculés à partir de deux nombres : le nombre de dimensions du système physique et la dimension n du paramètre d’ordre.

2.4.       Les raisons thermodynamiques d’une transition de phase

Après avoir introduit la transition de phase en partant de la fonction G, il est intéressant d’approfondir les raisons thermodynamiques qui provoquent cette transition, pour une transformation du premier ordre, ce qui nous amène à préciser la distinction entre instabilité et métastabilité [24].

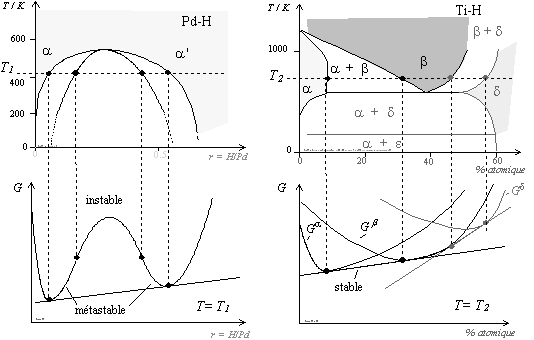
            Au cours de cette analyse, nous maintenons le système dans le domaine de l’équilibre, ou proche de l’équilibre. On se référera aux diagrammes de la figure 4 qui représentent la variation de l’enthalpie libre en fonction du rapport atomique H/M pour un système métal-hydrogène présentant une lacune de miscibilité (Pd-H), et pour un système possédant un changement structural du sous-réseau métallique en cours d’hydrogénation (Ti-H). La présence d’une nouvelle structure se traduit par les tracés séparés de Ga et Gb, enthalpies libres des deux phases a et b.

 

Figure 4a. Système présentant une lacune de miscibilité. Diagramme de phases du système Pd-H d’après [25].

Figure 4b. Système présentant une transformation structurale. Diagramme de phases du système Ti-H d’après [26].

 

            La transition de phase a lieu pour deux raisons bien distinctes : l’une des phases du système pénètre un domaine d’instabilité thermodynamique (décomposition spinodale), ou bien l’ensemble des phases du système diminue sa fonction intégrale G en provoquant une transition. Dans ce dernier cas, il s’agit du meilleur choix possible pour le système, qui n’est cependant pas obligatoire.

 

            La première raison (condition d’instabilité) est une cause impérative de décomposition de la phase. Cet effet se traduit par la séparation en deux phases isomorphes. Elle engendre deux phases cristallines de même structure mais distinctes en composition. Il s’agit d’une décomposition spinodale. Le diagramme de phases correspondant est représenté sur la figure 4a. Si le système de composition r0 est à la température T0 puis trempé à la température T1, la composition initiale reste homogène, alors que son enthalpie libre est localisée sur la courbe G, où il se retrouve immédiatement dans une configuration instable. Les fluctuations de composition provoquent immédiatement la démixtion, abaissant ainsi l’énergie libre totale du système. Pour cette composition, la démixtion se produit sans avoir à vaincre une barrière énergétique. Cela se produit chaque fois que  . La limite d’instabilité est indiquée par les traits pointillés qui représentent le lieu des points où . Pour les compositions initiales comprises entre la courbe binodale et la spinodale, le système est métastable,  . La transformation procédera dans ce dernier cas par un processus de nucléation et croissance.

            Pour la transition impliquant deux phases de structures différentes, nous rappelons que le maintien de la configuration initiale est possible. Il n’y a donc aucune obligation. C’est ce que l’on pourra observer s’il y a un retard à la germination d’une nouvelle phase ou lorsque la force motrice de la transformation est faible. Finalement, notons également que si l’équilibre thermodynamique le moins bas dans l’échelle des G se maintient après transformation, nous qualifierons cet état d’équilibre métastable. Il faut se garder de voir dans métastable quelque notion d’état transitoire.

2.5.       Transition de phase due aux interactions élastiques : système Métal - Hydrogène

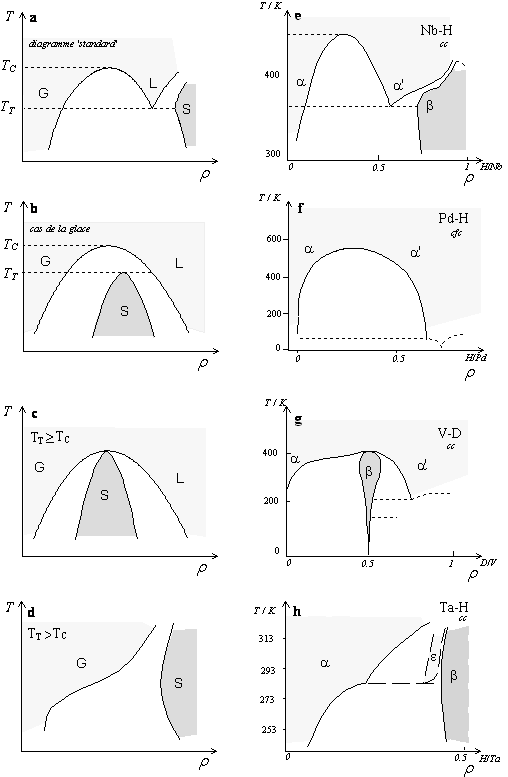
Alefeld a été le premier à remarquer la similitude entre la topologie (morphologie) des diagrammes de phases pour les transitions solide - liquide - gaz des systèmes à un seul constituant et les systèmes métal-hydrogène [28]. Nous avons reproduit schématiquement sur la figure 5 les diagrammes concernés sur lesquels, pour la comparaison, l’ordonnée est la température, l’abscisse la densité. TT et TC caractérisent le point triple et le point critique.

 

            Le schéma (a), représente un comportement ‘standard’ où la densité rS du solide est supérieure à celle rL du liquide. Dans le cas inverse, représenté sur le schéma (b), (glace, Si, Ge...) le domaine solide sera à l’intérieur de la courbe de coexistence. Par comparaison avec les systèmes M-H, sur le schéma (e) le point triple standard devient le point eutectique alors que le point triple de la glace deviendrait un point péritectique dans le schéma (g).

            Le système Pd-H, schéma (f), de structure c.f.c. s’apparente pour T >100K uniquement à la transition liquide - gaz du schéma (b). Le cas du système Nb-H, schéma (e), c.c, se confond avec le cas standard (a). L’analogie entre les différentes phases est immédiate : la phase a correspond au gaz, la phase a’ au liquide, et la phase b au solide. L’analogie entre les systèmes suggère pour Nb-H le cas où rS > rL avec TC > TT , pour Ta-H on aurait aussi rS > rL mais avec TC < TT . Le système V-H suggère par contre TC < TT et rS < rL . Le diagramme Pd‑H, lui, ne montrerait que la transition gaz - liquide.

 

Figures 5a, b, c, d. Diagrammes de phases pour des systèmes à un seul constituant.

Figures 5e, f, g, h.  r est la densité du système solide-gaz. Les rapports atomiques sont portés à titre indicatif.

Diagrammes de phases e, f, g : [25] ,  h : [30].

 

 

            Une des raisons évoquées pour expliquer la présence de diagrammes plus complexes pour les systèmes c.c. par rapport aux c.f.c. vient de l’augmentation du nombre de degrés de liberté dans la structure c.c. Cette dernière dispose de 3 sites octaédriques et 6 sites tétraédriques alors que la structure c.f.c. ne dispose que d’un site octaédrique et de deux sites tétraédriques [25].

 

            Alefeld [28] a appliqué la théorie élastique des défauts de Eshelby [29] et a démontré que l’interaction élastique apportait une contribution importante à l’interaction attractive conduisant à la transformation / condensation. En effet, lorsqu’un atome d’hydrogène est en position interstitielle, l’environnement local est déformé par sa présence, provoquant un déplacement des atomes métalliques premiers voisins. En retour, ces déplacements interagissent avec la couche suivante et ainsi de suite. Nous sommes en présence d’interactions à longue portée dont l’amplitude du champ de déformation est proportionnelle à 1/r2. Ce champ est caractérisé par une quantité : le tenseur du moment dipolaire élastique. L’interaction entre atomes d’hydrogène due aux champs de déformation à longue portée a donc été estimée à partir de l’interaction dipôle élastique - dipôle élastique. Ainsi Alefeld a démontré que l’interaction élastique apportait une contribution importante à l’enthalpie de solution. Cette analyse fut poursuivie par Wagner et Horner [31] qui ont introduit la discrétisation du réseau, non prise en considération dans le modèle initial.

            Bien qu’il soit donc possible en première approximation de calculer l’ordre de grandeur de la contribution élastique, et qu’elle puisse servir de guide à l’existence de phase, il ne faut pas oublier le rôle de la contribution électronique, tout aussi importante, comme ont pu le montrer les calculs de structure électronique, tant pour les systèmes métalliques [32], qu’intermétalliques [33][34].

2.6.       Extension de la théorie de Landau aux transitions de premier ordre

Nous présentons dans ce paragraphe un aperçu de la théorie de Landau étendue aux transitions de premier ordre. Cette approche permet, sous certaines conditions, de faire le lien entre la transition du premier ordre et la présence d’hystérésis [21][35].

 

            Dans son principe, Landau propose que l’on développe le potentiel thermodynamique G en série de Taylor, en fonction du paramètre d’ordre h, au voisinage du point critique. Pour les transitions du second ordre, des arguments de symétrie imposent que G soit une fonction paire du paramètre d’ordre h. G se met donc sous la forme :

                                                             (6)

            Pour satisfaire ce type de développement Landau suppose à priori que le développement est convergent. Or, pour répondre au problème de divergence à TC , Landau admet que les termes d’ordre supérieur sont sources de singularités et qu’en conséquence on peut se satisfaire des premiers termes pour effectuer les calculs. Finalement en tenant compte des valeurs du paramètre d’ordre à l’équilibre (h = 0 pour T > TC ; h ¹ 0 pour T < TC) et en négligeant l’influence de la pression lors de la transition, on montre que (6) peut se réduire, à l’expression :

                                                                     (7)

                        avec l2 et l4 > 0.

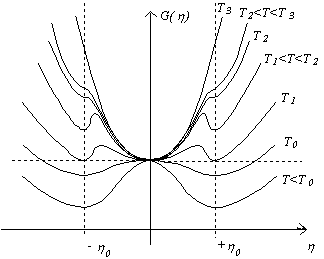
Dans ce cas, la forme du potentiel pour différentes températures est illustrée sur la figure 6.

Pour T<TC, il existe deux minima symétriques :

                                                         ,                                                (7b)

h0 s’annule en TC et pour T > TC  il n’y a plus qu’un minimum en h = 0. h s’annule continûment à TC , nous avons une transition du 2eme ordre induite par la température. En écrivant les dérivées successives pour satisfaire l’état d’équilibre on détermine les caractéristiques de la transition du deuxième ordre.

 

 

Figure 6.

Forme du potentiel (7) pour différentes températures.

 

 

 

            Pour étendre cette théorie et l’appliquer aux transitions de premier ordre, il faut bien évidemment admettre que le concept de paramètre d’ordre est maintenu et que l’on puisse toujours développer le potentiel thermodynamique en série de Taylor au voisinage de la température T0. De plus, on doit également être capable de retrouver la discontinuité caractérisant une transition de premier ordre, h s’annulant de façon discontinue.

Le développement du potentiel G est alors donné par la forme de Devonshire [36] :

                                                             (8)

                                                                                              avec d2, d4, d6 > 0.

            Dans cette expression T0 représente la température de changement de signe de la concavité en h = 0. Pour T > T0, G présente trois minima. La fonction G est représentée sur la figure 7, pour différentes températures. La transition à l’équilibre sera observée pour T1 , cas où la variable h produit la même valeur de la fonction G pour les trois minima. Soit :

                                     ,                           (9)

qui admet les solutions (pour les minima) :

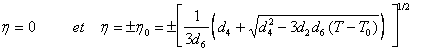                                 (10)

·      Pour, G n’admet qu’un seul minimum correspondant à la phase haute température , en h = 0. Les minima latéraux () deviennent instables.

·      A , les deux phases sont en équilibre, T1 est la température de transition.

·      Sur le domaine T0 < T < T1, les minima latéraux () sont stables, l’état h = 0 est métastable.

·      Inversement, pour T1 < T < T2, la situation correspond à des minima latéraux métastables et à une phase haute température (h = 0) stable.

·      Pour T < T0, seule la phase basse température correspondant aux minima  se retrouve à l’équilibre stable, la phase haute température devenant instable.

·      La température est celle au delà de laquelle la courbe décrivant G devient convexe, il n’y a plus de points d’inflexion.

 

 

 

 

Figure 7.

Forme du potentiel (8) pour différentes températures.

 

 

            Les états décrits ci dessus sont représentés sur la figure 8 où le paramètre d’ordre h et CP sont tracés en fonction de la température.

 

Figure 8a. La capacité calorifique présente une discontinuité caractéristique d’une transition de 1er ordre pour une transition à l’équilibre ( T1 )

Figure 8b.On peut avoir un phénomène d’hystérésis associé à la transition sur le domaine [T0 T2].seule la transition à T1 est réversible.

 

            Nous sommes en présence d’une transition de phase du 1er ordre induite par la température. La présence de métastabilité sur le domaine [T0 T2] permet, avec cette forme de potentiel, d’observer un phénomène d’hystérésis thermique : la transition de la phase désordonnée vers la phase ordonnée a lieu pour une température comprise dans le domaine [T1 T2] et la transformation inverse prend place pour une température située sur le domaine [T0 T1]. Les températures de transition ne sont pas identiques au refroidissement et à l’échauffement. On trouvera en annexe A à ce chapitre des compléments concernant l’hystérésis induite par l’application d’un champ externe à un système décrit par le potentiel (8).

3.    L’hystérésis

3.1.       Définitions

Au cours des paragraphes précédents, nous avons montré que des états métastables étaient associés aux transitions de premier ordre, en raison des discontinuités observées dans les dérivées premières de l’enthalpie libre. Généralisant cette observation, toute transformation du premier ordre rencontrée dans les systèmes à lacune de miscibilité ou dans les transitions de phase impliquant des structures différentes présente de la métastabilité. Ceci implique que la compréhension de la métastabilité est indissociable de la compréhension de l’hystérésis.

            Reprenons le schéma de la figure 8, où nous représentons la variable y en fonction de la variable indépendante x.

 

Figure 9a. Domaines de stabilité-métastabilité

Figure 9b. Trajets internes.

Figure 9c. Cas réel

 

            Considérons une transformation a ® b et suivons l’évolution du système depuis le point A(x1), représentatif de la phase a stable. Lorsque la variable indépendante x croît, le système suit le chemin AB, domaine de métastabilité. La transformation a ® b a lieu à la valeur x2, suivant la trajectoire BC. Si la variable indépendante suit exactement le chemin inverse, de x2 vers x1 , la variable y prend des valeurs différentes. Le chemin est alors caractérisé par la branche métastable CD de la phase b puis par la transformation b ® a à la valeur x1, suivant la trajectoire DA. Cette situation se retrouve pour les systèmes métal-hydrogène présentant de l’hystérésis, x correspond à la pression d’hydrogène, y à la composition de l’hydrure. ABCDA représente un cycle complet d’hystérésis. Cette définition du cycle obéit à deux critères essentiels :

·      le cycle doit être parcouru de manière quasistatique,

·      le cycle doit être reproductible lors de la production de n cycles, puisque l’hystérésis est une propriété intrinsèque du système.

Cette définition non ambiguë du cycle d’hystérésis a maintes fois été oubliée ces dernières années dans de nombreuses caractérisations thermodynamiques.

 

            Un certain nombre de propriétés sont associées au cycle d’hystérésis. Un cycle est toujours parcouru dans le même sens. Il se compose de deux branches réversibles AB et CD (états métastables a, b) et de deux branches irréversibles BC, DA (transformation a ® b et b ® a). Enfin, le cycle peut ne pas être parcouru complètement. Il est possible d’exécuter des trajectoires à l’intérieur d’un cycle (on parle dans ce cas de boucle interne, par exemple : boucle abcda). La boucle peut partir de l’une ou l’autre branche irréversible. Les chemins internes sont tracés pour un cas idéal, cd et ab, (figure 9b) et réel, boucle ijkl, (figure 9c). On voit apparaître un comportement réversible dans le cas idéal, qui se transforme en chemin irréversible dans le cas réel à mesure que l’on se rapproche de la branche opposée au point de départ. Cette dernière observation est importante, car dans l’hypothèse du cycle d’hystérésis unique et reproductible, le système doit repasser obligatoirement par le point i lorsque la boucle interne est décrite. Au cours de cet exposé nous avons volontairement ignoré l’état d’équilibre ‘absolu’ du système puisque nous ignorons tout de sa localisation, sinon qu’il devrait se situer quelque part à l’intérieur du cycle [2][44].

3.2.       OBSERVATIONs EXPérimentales - classification

La caractérisation thermodynamique des systèmes métal - hydrogène ou composés intermétalliques - hydrogène est faite dans la plupart des cas à partir des diagrammes dits « d’équilibre » , où la pression est mesurée pour une série de températures. Les résultats s’obtiennent par volumétrie, thermogravimétrie [37] ou plus rarement par volumétrie couplée avec un microcalorimètre [38][39]. Pour les systèmes extrêmement stables ou bien à basse température, les transitions de phases induites par l’absorption d’hydrogène sont détectées par des mesures de résistivité [40][41]. Par convention, on porte la pression sur l’axe des ordonnées et la composition sur l’axe des abscisses. Nous avons donc opté pour ce type de représentation pour la suite de l’exposé.

            Les conditions expérimentales permettent de distinguer quatre catégories relatives à la manifestation de l’hystérésis :

·      l’hystérésis de pression, résultante d’expériences isothermes,

·      l’hystérésis de solubilité ou de précipitation,

·      l’hystérésis thermique, observée pour des expériences isobares,

·      l’hystérésis observée lorsque le système est à composition constante.

 

Figure 10. Différentes manifestations du phénomène d’hystérésis.

En général les moyens d’investigation dépendent du type de système étudié. La plus ou moins grande stabilité du système et l’étendue du domaine d’existence de la solution solide sont des critères de choix pour la méthode employée. Cette tentative de classification ne tient pas compte des études effectuées à très haute pression d’hydrogène [25].

3.2.1.    L’hystérésis de pression

L’hystérésis de pression, figure 10a, représente la méthode la plus utilisée pour aborder la caractérisation thermodynamique de la transformation de phase. La teneur en hydrogène est modifiée afin de mesurer la pression de plateau, dans le domaine biphasé, au cours de la formation et de la décomposition de l’hydrure. Le rapport des pressions d’absorption et de désorption (Pabs/Pdes) sert à caractériser l’étendue du domaine. On voit également que l’hystérésis se manifeste au niveau des limites de phases : elles sont différentes à l’absorption et à la désorption, tant du côté de la solution que du côté de l’hydrure. On notera que la composition limite de phase en absorption est supérieure à la composition limite de phase en désorption. Il en résulte, en toute rigueur, que le comportement de chaque système métal - hydrogène doit être représenté par deux diagrammes de phases, l’un issu des isothermes d’absorption, l’autre des isothermes de désorption. Les travaux sur les systèmes Pd-H2 et Pd-D2 effectués par Wicke et Blaurock [42] représentés sur la figure 11 illustrent parfaitement ce comportement.

       

Figure 11. : Diagrammes de phases pour les systèmes Pd-D2 et Pd-H2 , d’après [42].

 

Rappelons que le système Pd-H2 présente une lacune de miscibilité et se distingue en conséquence par l’existence d’un point critique. Pour ce système, les températures critiques sont les mêmes en absorption et en désorption mais sont observées pour des compositions différentes, nC = 0,257 pour la désorption et nC = 0,295 pour l’absorption. Bien évidemment, l’hystérésis disparaît à la température critique.

            L’étendue du domaine (Pabs/Pdes) varie avec la température. Toutefois, mis à part le système Pd-H2 et U-H2 , pour les métaux, on dispose rarement de données complètes sur l’absorption et la désorption. Les informations disponibles dans la littérature, pour les systèmes composés intermétalliques - hydrogène, bien qu’abondantes, sont affligées de problèmes de reproductibilité et concernent souvent la réaction de désorption seule. Le tableau 1 ci-après donne une liste indicative des propriétés de divers systèmes. L’hystérésis en pression est caractérisée par la valeur ln(Pabs/Pdes).

Formule

Domaine T / K

Domaine P /bar

ln (Pabs/Pdes)

Réf.

Pd

300-556 (TC)

0.019-12

0.64-0

[44]

Pd1-x-Ptx

x = 0.05

283

0.025

0.65

[45]

 

x = 0.072

 

0.056

0.340

 

 

x = 0.10

 

0.16

0.17

 

 

x = 0.125

 

0.5

0.12

 

 

x = 0.15

 

1.25

non observé

 

Pd1-x-Nix

x = 0

273

0.013/0.0025

1

[46]

 

x = 0.05

 

0.030/0.02

0.96

 

 

x = 0.09

 

0.081/0.2

0.87

 

 

x = 0.15

 

0.21/2

0.51

 

 

x = 0.20

 

0.43/10

0.55

 

 

x = 0.25

 

0.72/25

0.75

 

U

723 - 923

0.057 - 22

1.0 - 0

[47]

Ti (b®g)

700 - 909

0.0013 - 0.893

0.94

[47]

V

313 - 373

3.7 - 47

0.7 - 0.2

[48]*

LaNi5

298 - 338

1.8 - 7.8

0.13

[49]*

LaNi4.8Sn.2

273 - 513

.13 - 100

0.23 - 0

[50]

LaNi5-xSn.x

x = 0.1

373

15

0.28

[51]

 

x = 0.2

 

8

0.16

 

 

x = 0.25

 

5.4

0.15

 

 

x = 0.32

 

4.1

0.08

 

 

x = 0.4

 

2.3

0.05

 

 

x = 0.5

 

1.3

0.04

 

LaNi4.7Al.3

298 - 448

.42 - 42

0.05

[52]*

LaNi4.25Al.25

213

0.054

0.23

[53]*

LaNi4.6Mn.4

298 - 248

0.15 - 1.5

0.1

[54]*

LaNi3Co2

298

0.23

0.16

[55]*

TiFe (b)

273 - 343

1.4 - 17

0.64

[56]*

TiFe.8Ni.2 (a®b)

323 - 370

0.33 - 2.45

0.05

[52]*

TiFe.9Mn.1 (b)

273 - 333

0.9 - 9.2

0.62

[52]*

(V.9Ti.1).95Fe.05

353

9.0

0.80

[57]*

TiMn1.5

273 - 323

2.96 - 19

0.93

[58]*

ZrNi

373 - 523

.00022 - .263

1.47

[59]*

ZrMn2

323 - 353

.007 - 0.03

0.99

[60]*

CaNi5 (b®g)

298 - 353

.51 - 3.5

0.16

[61]*

SmCo5

293 - 353

3.2 - 38

0.15

[62]*

Tableau 1. Les pressions sont évaluées autant que possible à mi-plateau, pour des tracés isothermes.

                     * : information provenant d’une base de données en [63]. Ces résultats sont indicatifs

 

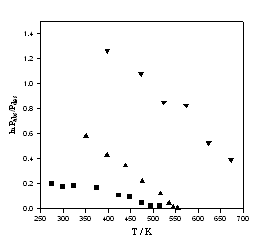
Dantzer et al. [64] ont démontré qu’il était possible de satisfaire le problème de reproductibilité du cycle à condition de minimiser le couplage entre les transferts de masse et de chaleur. Cette contrainte est d’autant plus importante pour les milieux pulvérulents. Il a été montré que les cycles doivent être produits en continu afin de maintenir la concentration de défauts - essentiellement des dislocations - à niveau constant ou à saturation. On voit émerger le rôle important de la microstructure. Généralement, l’étendue du domaine d’hystérésis diminue avec l’augmentation de la température, figure 12. Aux basses températures, les variations restent faibles. Aucune corrélation n’a été proposée jusqu’à maintenant.

 

 

 

Figure 12.

Évolution de l’hystérésis, ln(Pabs/Pdes) en fonction de la température. Pour les systèmes LaNi4.8Sn.2 - H2 (a®b) (n) [50] et ZrNi - H2 (b®g) (t) [66], les pressions sont évaluées à mi-plateau à partir des isothermes. Les données pour Pd - D2 (s) sont d’après[43].

 

3.2.2.    L’hystérésis de solubilité / précipitation

L’hystérésis de solubilité / précipitation se caractérise par la formation, à la température Th, d’une nouvelle phase à partir d’une phase homogène en cours de refroidissement, alors que cette nouvelle phase se décomposera en cours de chauffe à la température Tl. La différence DT = Th-Tl caractérise l’hystérésis rencontrée au cours de cette séquence. La représentation schématique correspond à la figure 10b.

            Cette méthode est tout particulièrement bien adaptée pour rechercher les paramètres thermodynamiques caractéristiques des systèmes très stables ou bien lorsque l’on veut opérer à basse température ou encore lorsque le domaine d’extension de la solution solide est réduit. Remarquons que dans les deux premiers cas, les mesures de pression sont plus contraignantes et la désorption sera pénalisée par des effets cinétiques.

            Expérimentalement, les températures de transition sont détectées par DSC, par des mesures de variations de résistivité [40][41], pour des échantillons préparés à plusieurs compositions. L’enthalpie de solubilité DHsol peut être déduite de la pente d’un tracé de van’t Hoff où la limite de solubilité est tracée en fonction de 1/T, pour la chauffe et le refroidissement, figure 13b. DHsol représente l’enthalpie mise en jeu lorsqu’un atome d’hydrogène est transféré de la phase hydrure à la solution solide. La relation entre l’enthalpie à dilution infinie DHH¥, l’enthalpie de transformation DHb®a et DHsol s’écrit :

                                                          DHsol = DHb®a - DHH¥                                                

            Puisque ces mesures sont réalisées pour des systèmes très stables, les enthalpies de transformation doivent être mesurées directement par calorimétrie. C’est le cas pour les systèmes tels que Ti-H [67], Zr-H [68], Y-H [69], La-H [70].

 

            Notons que dans les études de solubilité, le rôle de l’hystérésis a été jusqu’alors quelque peu ignoré. Les raisons évoquées se trouvent dans les difficultés d’accéder à des mesures précises qui nécessitent des équipements de qualité. L’hystérésis de solubilité est un paramètre technologique important pour le zirconium et certains de ses alliages, utilisés soit dans l’industrie nucléaire, soit pour l’élaboration du titane et ses alliages, très répandus dans la construction aéronautique. Dans ce cas, l’objectif principal est d’éviter la fragilisation du matériau par l’hydrogène. En effet, l’hydrogène dissous est attiré vers les domaines où s’exerce un champ de contrainte, pouvant aller jusqu’à la précipitation de la phase hydrure et provoquer la rupture. Il est évident que dans ces conditions, l’hystérésis de solubilité doit être déterminée précisément. Puls et al [71] [72] ont produit, au cours de ces dernières années, un travail théorique et expérimental extrêmement important sur ce problème spécifique.

 

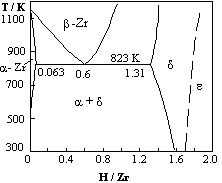
Figure 13a : Diagramme de phase schématique du système Zr-H.(d’après [73]).

 

Figure 13b. : système Zr - H; frontière  sous forme de courbes de van’t Hoff; la ligne continue représente le meilleur fit. Les lignes de solvus pour le refroidissement et pour le chauffage sont indiquées [68].

 

 

 

3.2.3.    L’hystérésis thermique

L’hystérésis thermique reportée pour la transformation de phase est schématisée sur la figure 10c. Les données issues de cette technique sont très peu nombreuses dans la littérature. Des boucles isobares ont été effectuées pour les systèmes Pd-H [2] et ZrNi-H [66] . Dans ce dernier cas, l’auteur affirme être le premier à avoir réalisé une boucle isobare pour le cas d’un composé intermétallique. Il est vrai que maintenir la pression constante tout en modifiant la teneur en hydrogène du système étudié demande un investissement expérimental important, alors que les mêmes informations peuvent être obtenues à partir des équations d’état du système, équations numériques déduites des isothermes.

            Il est important de posséder des données précises relatives à l’hystérésis thermique pour certaines applications à base d’hydrures telles que les machines chimiques à hydrure [74]. Le fonctionnement d’un transformateur de chaleur est schématisé sur la figure 14. On voit que la connaissance de l’hystérésis dT, pour des niveaux de pression constants, permet d’accéder aux conditions optimales de fonctionnement de la machine.

 

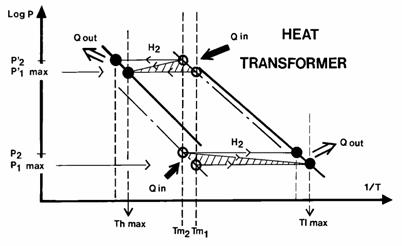
Figure 14. . Transformateur de chaleur en présence d’hystérésis; (·) en absorption; (o) en désorption; pour un transfert sous DP nul, Tm1 fournit les valeurs minimales Thmax et Tlmax. D’après [75].

 

3.2.4.    Hystérésis à composition constante

Cette forme d’hystérésis peut être observée dans les systèmes où les diagrammes de phases présentent des points eutectoïdes, comme pour le système Zr-H, figure 13a. Des températures de transitions de 833K au chauffage et de 809 K au refroidissement ont été reportées pour le point eutectoïde [68].

3.2.5.    Influence de la microstructure

Beaucoup d’études ont été effectuées  sur les systèmes métal - hydrogène et pourtant, comme nous l’avons déjà souligné à plusieurs reprises, l’influence de l’hystérésis sur les observations expérimentales doit impérativement être prise en considération. Les résultats les plus complets sont accessibles pour le système Pd - H. D’autres systèmes métalliques (Ti, Zr) ont trouvé un regain d’intérêt et ont été abordés plus rigoureusement, en raison de leur impact technologique. Bien évidemment, ces remarques s’appliquent aux systèmes composés intermétalliques - hydrogène où la production de composé hydruré pulvérulent complique davantage les études. Au cours de ces dernières années, les efforts ont surtout porté sur la mise au point de nouvelles techniques pour progresser dans la caractérisation thermodynamique [38] , thermique [76] , et microstructurale [19][20].

            D’une façon générale, la présence d’une phase gazeuse comme agent réactionnel ne permet pas d’opérer dans des conditions thermodynamiques rigoureusement contrôlées lorsque l’on travaille sur les grands instruments (neutron, exafs...) ou si l’on désire approfondir l’étude de la microstructure du matériau par microscopie électronique. Les matériaux stables offrent un bon compromis. Pour des pressions voisines de l’atmosphère, la surface du composé hydruré pourra être empoisonnée par du dioxyde de soufre afin de limiter le dégazage en hydrogène [17]. Néanmoins des informations importantes ont été obtenues en microscopie électronique pour le système Pd-H. Après un cycle complet, Wise et al [77] ont montré la formation de dislocations, dont la densité serait comparable à celle obtenue après un laminage à froid du palladium. Des études microstructurales ont été publiées récemment concernant les systèmes intermétalliques ZrNi-H [78] et LaNi5-H [19] [20]. Ces travaux témoignent de la difficulté de la technique à mettre en oeuvre, mais également de l’importance des problèmes à traiter, afin de mieux comprendre le lien entre la formation d’un composé hydruré et l’évolution de sa microstructure.

            Ainsi, il a été prouvé que l’étendue du domaine d’hystérésis était liée à la morphologie du matériau. Il est bien établi que l’hystérésis diminue lorsque l’on passe du matériau solide recuit au matériau défectueux ou divisé.

            Chercher à comprendre l’hystérésis implique également des études plus approfondies sur l’évolution de la structure au cours de la transformation, que ce soit pour les systèmes à lacune de miscibilité (Pd-H) dont l’accroissement de volume au cours de l’hydruration peut être considéré comme isotrope, ou pour les systèmes présentant une transformation structurale du sous-réseau métallique (U-H, Ti-H, Zr-H). On pourrait penser que l’importance des variations de volume enregistrées pendant le cycle d’hydruration / déhydruration est reliée à l’étendue du domaine de l’hystérésis. Il n’en est rien, ou tout au moins, la corrélation que l’on peut extraire d’un système tel que Pd-H, se trouve parfois en contradiction avec un autre système, par exemple V‑H.

3.3.       THERMODYNAMIQUE DE l’hystérésis

L’analyse thermodynamique des systèmes interstitiels métal - hydrogène a été développée dans la thèse de H.Y.Cai [1]. Toutes les équations caractéristiques faisant appel aux fonctions thermodynamiques ont été dérivées en se basant sur le principe de Gibbs concernant l’égalité des potentiels chimiques des différents constituants des phases à l’équilibre thermodynamique. En toute rigueur, cette hypothèse n’est pas satisfaite pendant la transformation puisque le système n’est pas à l’équilibre. Considérons la transformation en régime isotherme, figure 10a, le potentiel chimique de l’hydrogène est plus élevé pendant la phase de formation de l’hydrure que pendant sa décomposition. Les réactions s’écrivent :

                                                                               (13)

pour la formation de l’hydrure à partir de la solution solide saturée et

                                                                              (14)

pour la décomposition de l’hydrure.

            En conservant le formalisme appliqué en [1], a, a’, b, b’ sont exprimés par le rapport  nH/nC  où nH est le nombre de mole d’atomes d’hydrogène et nC le nombres de mole d’atomes métalliques (nC = 6 pour le LaNi5). Pabs et Pdes représentent les pressions de plateau de formation et décomposition. Les variations d’enthalpies libres pour les réactions (13) et (14) s’écrivent

                                            et                                   (15)

Les DGi sont exprimées par mole d’hydrogène gazeux et par rapport à l’état standard de l’hydrogène gazeux, alors que le gaz est supposé suivre un comportement idéal.

            En fait, pendant la transition, le système est constitué de trois phases, les deux phases solides et la phase gazeuse et de deux constituants, l’hydrogène et le métal (ou composé intermétallique). Dans ces conditions, la règle des phases de Gibbs impose un seul degré de liberté (v = c + 2 - f), la pression doit rester constante pendant la transition. En fait la présence d’hystérésis impose un degré de liberté supplémentaire puisque Pabs ¹ Pdes. Par la suite nous évaluerons le coût de l’irréversibilité, indissociable de l’hystérésis.

3.3.1.     Hystérésis et production d’entropie

L’analyse thermodynamique que nous présentons ne requiert pas la connaissance de l’origine de l’hystérésis. Elle permet de calculer la production d’entropie, contribution irréversible, pendant la réalisation d’un cycle complet.

            Suivant Prigogine et Defay [79][80], la variation d’entropie d’un système fermé peut être scindée en deux contributions. En désignant par deS le flux d’entropie dû aux échanges avec l’extérieur et par diS la contribution résultant des transformations internes, on écrit :

                                                                dS = deS + diS                                                       (16)

            L’accroissement d’entropie diS, dû aux modifications à l’intérieur du système, n’est jamais négatif. Il est nul lorsque le système ne subit que des transformations réversibles. Il est positif dans le cas de processus irréversibles.

                        processus réversible :             diS = 0

                        processus irréversible :           diS > 0                                                           (17)

Nous devons calculer la production totale d’entropie, lorsque le système décrit un cycle complet pour revenir à son état initial. Pour toute fonction d’état évaluée sur un cycle fermé nous pouvons écrire :

                                                                                                        (18)

            ainsi,

                                                                                                                       (19)

            L’équation (19) mérite quelques commentaires. Elle permet de calculer la production totale d’entropie. Pour cela, il suffira d’évaluer le flux d’entropie échangé entre le système et le milieu extérieur, soit :

                                                    et, donc :                                          (20)

où  représente l’énergie totale calorifique échangée pendant les différentes étapes du cycle. Si nous tenons compte du critère fondamental de reproductibilité du cycle, (19), pour chaque cycle réalisé, peut se mettre sous la forme

                                                                  ,                                                         (21)

pour des cycles identiques.

            Le non respect de cette condition implique nécessairement que d’autres phénomènes physiques mal contrôlés et non identifiés interviennent au cours de la réalisation du cycle. Notons que jusqu’à ce point, nous n’avons fait aucune restriction quant à la nature de l’hystérésis. Cette description globale s’applique donc à tout système présentant cette caractéristique. Revenons maintenant au système solide - gaz afin d’évaluer l’énergie dissipée ou perdue. Il est également important d’expliquer comment cette énergie est dissipée au cours des différentes étapes. Le traitement sera présenté pour le cas isotherme (hystérésis de pression) et isobare (hystérésis de température). Il restera donc à exploiter l’influence de l’irréversibilité sur la détermination des grandeurs thermodynamiques.

3.3.2.    Production d’entropie, cas isotherme

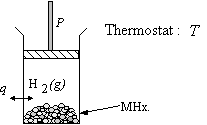
Envisageons premièrement un système modèle S, représenté sur la figure 15. Le système est un cylindre aux parois diathermes, fermé par un piston. Il contient le solide et le gaz. L’ensemble est immergé dans un thermostat à la température T. Le piston est supposé se déplacer sans frottement. Ce dispositif permet d’évaluer le travail échangé entre le système S et le milieu extérieur. La phase solide représente un système ouvert par rapport à la phase gazeuse, mais il est beaucoup plus simple de raisonner sur le système fermé gaz + solide afin d’évaluer les transferts énergétiques. Nous introduisons donc une contrainte sur le nombre de mole de chaque constituant. L’hydrogène se répartit entre la phase gazeuse et la phase solide. Enfin, nous considérons que le gaz suit la loi des gaz parfaits et nous négligeons le volume du solide devant le volume du gaz. Cette dernière hypothèse n’altère en rien la démonstration mais évite de prendre en considération des termes de travail non significatifs liés au volume du solide.

 

 

Figure 15 : Le système S est composé d’une mole de composé solide MHx et (1-x)/2 mole de gaz H2;  0£x£1.

 

 

 

Figure 16a. Cycle d’intégration dans le plan P,x.

Figure 16b. Cycle d’hystérésis isotherme.

 

Rappelons les relations (19 - 20),

                                                          ,                                                

qui exprime le lien entre la production d’entropie et les échanges avec l’extérieur. Par application du premier principe sur un cycle complet nous obtenons :

                                                                                                       (22)

ou encore :

                                                                                                                      (23)

soit :

                                                                                                                       (24)

L’équation (22) montre que le calcul du travail fourni au cours d’un cycle complet est directement lié aux échanges calorifiques pendant le cycle. Par la suite, nous ne tiendrons pas compte des différences de limite de phase entre l’absorption et la désorption, ce qui, là encore, simplifie le calcul. Nous supposerons de plus que le système se compose d’une mole de composé solide et une mole d’hydrogène atomique. La variable x représente le nombre de mole d’atomes d’hydrogène absorbé par mole de composé solide. Dans ces conditions le volume occupé par la phase gazeuse est donné par :

                                                                                                                         (25)

Les variables du système étant P,T,x, toute variation dV du volume de la phase gazeuse est donnée par :

                                                                        (26)

Dans les conditions isothermes, le travail effectué au cours du cycle complet se calcule facilement à l’aide de (25)

                                                               (27)

soit, après substitution :

                                                                                        (28)

Les bornes d’intégration sur le cycle, schématisé sur la figure 16, correspondent aux variables de la phase gazeuse; on choisit comme état initial le solide complètement désorbé à la pression Pdes , en 4.

                  (29)

soit :

                                                                                                              (30)

Si nous avions introduit les limites de phase rmin et rmax au lieu de 0 et 1, l’expression (29) conserverait la même forme :

                                                                                          (31)

Cette expression représente le travail fourni au cours du cycle exprimé en joule par mole d’hydrure. La pression d’absorption étant supérieure à la pression de désorption, la somme du travail fourni sur un cycle est positive : du travail est fourni au système. En appliquant (24), on obtient :

                                                                                                                (32)

De l’énergie a été dégradée au cours du cycle effectué par le système. Cette énergie est dissipée sous forme de chaleur comme l’indique (23). Soit :

                                                                                                            (33)

Au cours de l’évaluation du travail, chaque étape (compression, détente) a été produite de façon quasistatique et réversible. La production d’entropie ne peut que provenir des réactions de transformation dans le solide bien que cette entropie produite ne soit transmise au milieu extérieur que par l’intermédiaire de la phase gazeuse.

 

            Flanagan et al [2][44] ont abondamment travaillé sur la thermodynamique de l’hystérésis avec comme support le système Pd-H. Toutefois, les premières contributions ne sont pas exemptes de critiques. En effet, comme il a été remarqué par McKinnon [81], on ne peut pas mélanger dans le traitement des termes liés à l’équilibre et d’autres associés au non-équilibre. De même, il est difficile d’accepter un traitement qui fait appel au potentiel chimique des atomes métalliques à la vue des remarques que nous avons formulées au début de ce paragraphe. Dans leur dernier article de synthèse sur l’hystérésis dans les réactions à l’état solide, Flanagan et al [44] ont reformulé leur analyse en tenant compte des remarques antérieures. L’approche qui suit est issue de ces derniers travaux.

 

            Pour compléter cette analyse, il est nécessaire d’identifier les étapes du cycle au cours desquelles l’énergie est dissipée. Reprenons le système S et la description de son cycle d’hystérésis, figure 16, . Le cycle comprend deux étapes irréversibles (, formation de l’hydrure et , décomposition) et deux étapes réversibles ( et ) pour lesquelles sont associées les phases de compression et détente du gaz. Pour arriver à leur fin, Flanagan et al ont besoin d’introduire un chemin thermodynamique différent mais parcouru de manière réversible. Il est donc nécessaire de faire appel à une étape intermédiaire représentative de l’équilibre thermodynamique de la transformation. Dans ces conditions, on est amené à évaluer les grandeurs thermodynamiques DS et DG pour les différentes étapes de la transformation, mais en tenant compte du chemin hypothétique représentatif de l’équilibre.

                                     DS(1® 2) = DS(1® 5) + DS(5® 6) + DS(6® 2)                            (34a)

                        et

                                     DS(3® 4) = DS(3® 6) + DS(6® 5) + DS(5® 4)                           (34b)

                                                 (35)

Avec pour 1® 5, x=0 et pour 6® 2, x=1, on obtient :

                                                                                             (36)

Remarquons que l’enthalpie de la transformation s’écrira de la même façon :

                                    DH(1® 2) = DH(1® 5) + DH(5® 6) + DH(6® 2)                          (37a)

                                                             DH(1® 2) = DHeq                                                    (37b)

DH(1® 5) et DH(6® 2) sont nuls car nous avons supposé un comportement idéal du gaz et des conditions isothermes. La variation de l’énergie libre DG(1® 2) s’écrit à partir de (36) et (37)

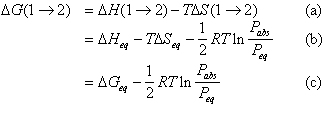                                                             (38)

Puisque DGeq = 0 , le système étant à l’équilibre, on obtient :

                                                                 

On peut exprimer, pour l’étape 1® 2 la production d’entropie en combinant l’équation (16) et le résultat (36)

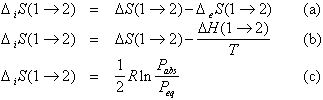                                                             (39)

Cette dernière quantité est, comme il se doit, positive. Elle est reliée à la variation d’énergie libre. En comparant (38) et (39) il vient :

                                                                                                 (40)

DG(1® 2) correspond à l’énergie libre dissipée au cours de la réaction de formation. En suivant la même démarche pour l’étape de décomposition de la phase hydrure, on obtient :

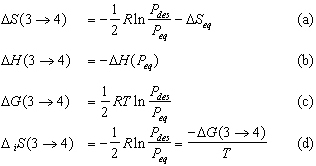                                                               (41)

Puisque pendant les étapes réversibles DiS = 0, la production totale d’entropie se réduit à :

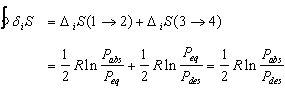                                                                       (42)

Nous avons vu de plus que l’irréversibilité n’apparaissait pas dans l’expression de la variation d’enthalpie, en conséquence, l’énergie libre dissipée s’écrit :

                                                                                        (43)

Rappelons que le système modèle S nous a permis de calculer le travail fourni pendant le cycle. Les équations (30) et (43) nous permettent alors d’écrire :

                                                                             (44)

Le seul travail produit durant le cycle correspond à la compression du gaz (4® 1) et à la détente (2® 3). La chaleur est dissipée uniquement pendant ces deux étapes réversibles et isothermes et pas pendant les étapes irréversibles. Ce résultat pour le moins surprenant mérite que l’on s’y attarde. Nous savons désormais que :

                        

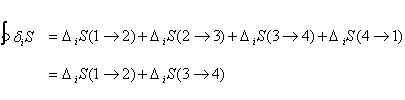
ou encore, exprimé à l’aide (16) :

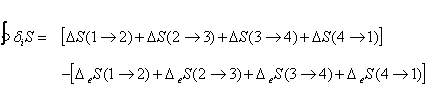                                   (46)

Or le premier terme représente la variation d’entropie du système sur le cycle, soit , le second représente le flux d’entropie vers le milieu extérieur, soit :

                                                                                   (47)

à l’aide de (36) :

                                                                                                          (48)

de même :

                                                                                                       (49)

soit :

                                                                                              (50)

et (46) se réduit à :

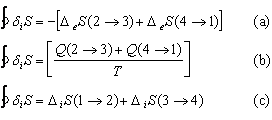                                                                          (51)

L’expression (51) explicite la production d’entropie pour les étapes (1® 2, 3® 4 ) et montre que l’énergie est dissipée au milieu extérieur pendant les étapes réversibles (2® 3, 4® 1)

3.3.3.    Production d’entropie, cas isobare

Reprenons le système S tel qu’il est décrit plus haut. Le piston maintient cette fois une pression fixe et la température du thermostat peut être modifiée de manière à faire évoluer l’état du système. Toutes les autres caractéristiques et approximations sont maintenues. Le cycle d’hystérésis thermique, décrit à pression constante, aura l’allure présenté sur la figure 17. Pour un cycle isobare le travail fourni au système est nul, soit :

                                                                                                                                (52)

Le cycle idéal effectué par le système a l’allure présenté sur la figure 17.

Figure 17a. Cycle d’hystérésis dans le plan (T,x).

Figure 17b. Cycle d’hystérésis isobare

 

On peut évaluer les échanges d’entropie du système au milieu extérieur, soit .

Pour les étapes réversibles, 4® 1 et 2® 3, on a :

                                       (57)

si on considère les CP constants, et,  de même :

                                                                       (58)

Pour les étapes irréversibles isobares et isothermes 1® 2 et 3® 4, on a :

                                                                             (59)

et

                                                                            (60)

Pour l’étape 5® 6, représentative de l’équilibre, la transformation est réversible. La variation d’entropie associée s’exprime par :

                                                                       (61)

pour une réaction à température constante :

                                                                                 (62)

On peut écrire :

                                                                                (63)

en écrivant :

                                                                  (64)

et par un calcul similaire aboutissant aux équations (57) et (58) ci-dessus, et à l’aide de (61), on obtient :

                (65)

en posant :

                                                                                    (66)

et en considérant (62) on aboutit à :

                                        (67)

de même :

                                         (68)

Soit :

                                                                    (69)

Cette formulation permet un calcul de l’entropie produite sur un cycle à partir de données expérimentales [2] et n’implique pas la connaissance de la température d’équilibre, à la différence de la perte d’énergie libre sur un cycle obtenue de (67) et (68) :

                                                                              (70)

            L’évaluation de (70) nécessite une estimation d’une température d’équilibre.

4.    Conclusion

Dans ce chapitre nous avons abordé l’aspect thermodynamique des transformations de phase, associées à la formation et à la décomposition de l’hydrure. Les transitions du premier ordre se distinguent dans la majorité des cas par la présence du phénomène d’hystérésis.

 

            Bien que très répandues, ces transitions du premier ordre ont été bien moins étudiées, tant sur le plan expérimental et théorique, que les transitions du second ordre. Toutefois, l’étude du potentiel de Landau étendu aux transitions du premier ordre montre que l’hystérésis devient une caractéristique de la transition de phase observée pour un paramètre d’ordre associé à l’état du système. La présence d’un potentiel non-convexe permet d’expliquer l’apparition de l’hystérésis mais reste limitée. En effet, un tel potentiel ne garantit pas en lui même l’apparition d’hystérésis dans un système. Il ne permet pas non plus d’expliquer ou de représenter les comportements complexes observés expérimentalement, notamment les trajectoires décrites à l’intérieur de la boucle principale d’hystérésis.

            Cette approche, complétée par un traitement thermodynamique du phénomène a permis d’établir le caractère dissipatif de l’irréversibilité de type hystérésis à travers l’évaluation de l’entropie produite. Cependant, cette estimation de la production d’entropie se calcule uniquement pour des systèmes décrivant des boucles d’hystérésis fermées, la localisation, voire l’existence d’états d’équilibres restant spéculatifs.

            Il est à noter que ces deux approches ne sont pas liées aux causes du phénomène.

            Dans l’optique de la modélisation de l’hystérésis, il apparaît nécessaire d’aborder l’hystérésis de manière rigoureuse afin d’identifier formellement ses propriétés. Ce travail fait l’objet du chapitre suivant.

Annexe A : Hystérésis et potentiel non-convexe

Reprenons l’expression du développement de Landau-Devonshire I.(8) exprimé en I.2.6. Dans le cas de la pression constante, on peut écrire le potentiel dépendant de la température sous la forme :

                                                                       (a)

                                                                                              avec d2, d4, d6 > 0.

Dans ce cas, les états d’équilibre isotherme de (a) sont donnés par :

                                                                                                                         (b)

L’ensemble des résultats obtenus est résumé sur la figure a, le potentiel est tracé pour diverses températures.

            Nous avons étudié en I.2.6. le cas de la transition de phase induite par la température et l’hystérésis associée.

            Pour compléter cette approche, nous considérons l’influence d’un champ externe F , thermodynamiquement conjugué du paramètre d’ordre ,  appliqué au système. Ce champ peut, par exemple, exprimer une dépendance en pression sous la forme . Ce potentiel apporte la contribution  à l’expression de l’énergie libre. Dans ce cas la forme de F devient :

                                                                                                       (c)

et la condition d’équilibre (b) s’écrit alors :

                                                                                                                        (d)

 

 

 

 

Figure a.

Tracé du potentiel (a) pour différentes températures.

 

 

 

            Sur les figures b,c,d,e,f, on a représenté le tracé de   , en fonction du paramètre d’ordre , pour différentes températures. Les flèches horizontales représentent l’amplitude maximale de l’hystérésis que peut présenter le système isotherme soumis à la variation du champ F. Les portions décroissantes des courbes, représentées en pointillés, représentent les états instables.

 

 

Figures b,c,d,e,f.

Tracés de  , en fonction du paramètre d’ordre , pour différentes températures.

 

b. T < T0

c. T0 < T < T1

d.  T1 < T < T2

e. T2 < T < T3

f. T3 < T

 

            Sur la figure b, T < T0 , O est instable, on peut observer une transition du premier ordre induite par F entre les minima symétriques +0 et -0 . Dans les cas c et d, T0 < T < T2, apparaît une nouvelle possibilité de transition du premier ordre induite par F entre O et  +0 ou -0 . En e, T2 < T < T3, seule la possibilité de transition entre O et  +0 ou -0 subsiste. Enfin, en f, T3 < T , il n’y a plus de possibilité de transition induite par le champ externe F.

 

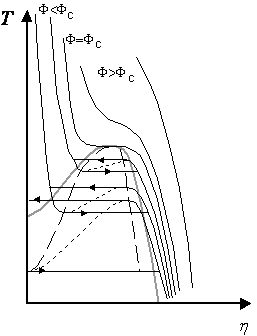
            La figure g décrit l’influence de la température sur la valeur d’équilibre du paramètre d’ordre , pour différentes valeurs positives du champ F. On observe un point critique au-delà duquel il n’y a plus de transition du premier ordre.

 

 

 

Figure g.

Valeur à l’équilibre du paramètre d’ordre en fonction de T pour différentes valeurs de F. On observe des transitions de premier ordre pour F<Fc .

 

La ligne spinodale (tirets) joint les extrémités des portions des courbes représentant les états instables (pointillés). La ligne représentant les positions des transitions à l’équilibre apparaît en grisé.

 

 

 

 

 

 

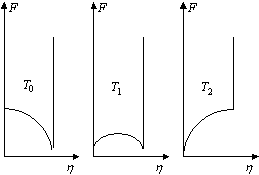
            De manière générale, l’emploi d’un potentiel non-convexe induit des effets d’hystérésis. Considérons le système de la figure h représentant F sous la forme d’un puits de potentiel double qui évolue avec la température. On obtient un cycle d’hystérésis maximale sous la forme d’une boucle carrée.

 

figure h.

Potentiel en double puits et hystérésis associée.

 

 

Références

[1]       H.Y. CAI, Contribution à l'étude thermodynamique et cinétique de l’hydruration des composés intermétalliques. Etude du composé LaNi5. Thèse de l'université Paris-Sud, Centre d'Orsay, (1995)

[2]       T.B. Flanagan, J.D. Clewley, T. Kuji, C.N. Park, J. Chem. Soc. Faraday Trans. 1, 82, 2589-2604, (1986)

[3]       P. SALOMONSSON, P. JOHANSSON, B. KASEMO, Catalysis Letters, 33, 1-13, (1995)

[4]       J. F. MARUCCO, J Solid State Chem. , 10, 211-218, (1974)

[5]       D. H. Everett, The Solid-Gas Interface, E. FLOOD, ed. , Marcel Dekker, N.Y. , vol. 2, 1055, (1967)

[6]       w. p. bryan, J. Chemical Education, 64, 209, (1967)

[7]       p. Ruetschi, f. meli, j. desilvestro, J. Power Sources, 57, 85-91, (1995)

[8]       n. furukawa, J. Power Sources, 51, 45-59, (1994)

[9]       h. kronberger, J. Applied Electrochem. , 26, 947-951, (1996)

[10]     M. LAtroche, A. Percheron-guégan, y. chabre, j. Bouet, J pannetier, E. ressouche, J. All. and Comp. , 231, 537-545, (1995)

[11]     R. B. SCHWARZ, Materials for hydride-based batteries, Los Alamos National Laboratory Communication, http://www.education.lanl.edu, (1997)

[12]     F. basile, J.  Appl. Electrochem. , 27, 598-604 (1997)

[13]     T. IMOTO, k. satoh, k. nishimura, t. yonesaki, s. fujitani, i. yonezu, J. All. and Comp. , 223, 60-64, (1995)

[14]     y. ohtani, s. hashimoto, h. uchida, J. Less-Comm. Met. , 172-174, 841-850 (1991)

[15]     h. uchida, S. SEKI, S. SETA, J. All. and Comp. , 231, 403-410, (1995)

[16]     l. grasjo, g. hultquist, k.l. tan, m. seo, Appl. Surf. Sci.  89, 21-34, (1995)

[17]     s. myhra, e.h. kisi, e.m. gray, J. All. and Comp. , 224, 305-315, (1995)

[18]     t. katrissios, e.h. kisi, s. myhra, J. Mater. Sci. , 30, 4973, (1995)

[19]     G.H. KIM, C.H. CHUN, s.G. lee, j.Y. lee, Acta. Met. Mater. , 9, 3157-3161, (1994)

[20]     G.H. KIM, s.G. lee, K.Y. LEE, C.H. CHUN,  j.Y. lee, Acta. Met. Mater. , 6, 2233-2240, (1995)

[21]     P. papon, j. leblond : Thermodynamique des états de la matière, Hermann (1990)

[22]     L. D. Landau : Phys. Z. Sowjetunion, 11, 26, (1937)

[23]     k.G. Wilson, Phys. Rev. B4, 3184, (1971)

[24]     D.A. Porter, K.E. Easterling, Phase Transformations in Metals and Alloys, Chapman & Hall, p117, (1993)

[25]     Y. FUKAI : The Metal-Hydrogen System, Springer series in material science 21, Springer (1993)

[26]     A. san-martin, F.d. manchester, Bull. All. Phase Diagrams, vol. 8 n°1, p30, (1987)

[27]     Y. FUKAI, J. Less-Comm. Met., 172-174, 8-19, (1991)

[28]     G. ALEFELD Berichte der Bunsen-Gesellschaft, 76(8), 746 (1972)

[29]     J.D.  Eshelby, Solid State Phys. , 3, 79, (1956)

[30]     T. Schober, H. Wenzl : dans Hydrogen in Metals II, Topics in Appl. Phys. , Vol 29, ed. G. Alefeld, J. Völkl, Springer (1978)

[31]     H. Wagner, H. Horner : Adv. Phys., 23, 587 (1974)

[32]     A.C. Switendick, (1972) : dans Hydrogen in Metals I, Topics in Appl. Phys., Vol 28, ed. G. Alefeld, J. Völkl, Springer (1978)

[33]     M. Gupta, J. Less-Comm Met. , 130, 219 (1987)

           M. GUPTA, dans Hydrogen in Intermetallic Compounds I, Topics in Appl. Phys. , Vol 63, ed. L. Schlapbach, Springer (1988)

[34]     T. suenobu, I. tanaka, h. adachi, G-y. adachi, J. All. and comp. , 221, 200-206, (1995)

[35]     J.C. Toledano, P. toledano : The Landau theory of phase transitions, World Scientific, Singapore (1987)

[36]     A.F. Devonshire, Adv. Phys. , 3, 85 (1954)

[37]     N. Gérard, S. Ono, Hydrogen in Intermetallic Compounds II, Topics in Appl. Phys. , Vol 67, Springer-Verlag, p.165 (1992).

[38]     P. Dantzer, A. Guillot, J. Phys. E: Sci. Instrum.  , 15, 1373 (1982)

[39]     P. Dantzer, F. Marcelet, J. Phys. E: Sci. Instrum.  , 18, 537 (1985)

[40]     P. Vajda, Chapter 137 in Handbook on the Physics and Chemistry of Rare Earths, Vol 20, Elsevier Science, p.207 (1995).

[41]     A.W. Szafranski, Polish J. Chem. , 69 , 1340-1347 (1995)

[42]     E. Wicke, J. Blaurock, Journal Less-Comm. met. , 130, 351, (1987)

[43]     J. Blaurock, thèse de doctorat, Westfälische Wilhelms-Universität Münster, (1985)

[44]     T. B. FLANAGAN, C. -N. PARK, W.A. OATES, Prog. Solid State Chem. 23, 291-363, (1995)

[45]     h. noh, T. B. FLANAGAN, T. SONOda, Y. sakamoto, J. of All. and Comp. , 228, 164-171, (1995)

[46]     T. B. FLANAGAN, h. noh, Z. Naturforsch. , 50a, 475-486, (1995)

[47]     W.M. Mueller, J.P. Blackledge, G.G. Libowitz, Metal Hydrides, Academic press, New York (1968)

[48]     J. J. Reilly, R.H. Wiswall, Inorg. Chem. , 9, p1678, (1970)

[49]     C.E Lundin, F.E. Lynch, Solid state hydrogen storage material for application to energy needs, Rept. AFSOR F44620-74-C0020, Denver Res. Inst. , jan. (1975)

[50]     S. Luo, W Luo, J.D. Clewley, T. B. FLANAGAN, R.C Bowman, J. All. and Comp. , 231, 473-478, (1995)

[51]     S. Luo, W. Luo, J.D. Clewley, T.B. FLANAGAN, L.a. wade, J. All. and Comp. , 231, 467-472, (1995)

[52]     E.L. Huston, G. Sandrock , J. Less-Comm Met. , 74, p435, (1980)

[53]     H. .Diaz, A. Percheron-Guegan, J.C. Achard, C. Chatillon, J.C. Mathieu, Int. J. Hydrogen Energy, 4, p445, (1979)

[54]     C.E Lundin, F.E. Lynch, In Proc. Miami Int. Conf. on Alternative Energy Sources, U. of Miami, p3803, (1978)

[55]     P.D. Goodell, G.D. Sandrock, E.L. Huston, Rept. SAND79-7095 , Sandia N. L. , jan. (1980)

[56]     J. J. Reilly, R.H. Wiswall, Inorg. Chem. , 13, p218, (1974)

[57]     J.F. Lynch, A.J. Maeland, G.G. Libowitz, Z. Phys. Chem. , NF, 145, p51, (1985)

[58]     t Gamo, y Moriwaki, N. Yanagihara, T. Yamashita, T Iwaki, In Proc. 3rd World Hydrogen Energy Conf. , Pergamon Press, p2127, (1981)

[59]     g.g. libowitz, h.f. hayes, T.R.P. gibb, The system Zirconium-Nickel and Hydrogen,  J. Phys. Chem. , 62, p76, (1958)

[60]     M. UCHIDA, S. SUDA,  Res. Repts. Kogakuin Univ. , 71, Oct., p41, (1958)

[61]     G. D. SANDROCK,  Proc. 12th IECEC, Am. Nuc. Soc. , Vol. I, p951, (1977)

[62]     F.A. Kuijpers, H.H. van Mal, J. Less-Common Met. , 23, p395, (1971)

[63]     Base de données réalisée sous la direction de G. SANDROCK et G THOMAS à Sandia National Laboratories : http://hydpark.ca.sandia.gov/

[64]     P. Dantzer, M. Pons et A. Guillot, Z. Phys. Chem. , 183, 205, (1994)

[65]     M. PONS : Transferts de chaleurs dans la poudre de LaNi5 et leur couplage avec la réaction d'hydruration, Thèse de l'Université Paris VI, (1991)

[66]     W Luo, A. CRAFT, T. KUJI, H.S. CHUNG, T.B. FLANAGAN, J.  Less-Comm. Met. , 162, 251-266, (1990)

[67]     P. Dantzer : J. Phys. Chem. Solids : 44, 913, (1983)

[68]     P. DANTZER, W. LUO, T. B. FLANAGAN et J. D. CLEWLEY, Metall. Trans. A, 24 1471-1479. (1993)

[69]     P. Dantzer, O. J. Kleppa, J. Chem. Phys. , 73, 5259 (1980)

[70]     P. Dantzer, O. J. Kleppa, J. Solid State Chem. , 35, 34 (1980)

[71]     S.-Q. Shi, M.P. Puls, J. Nucl. Mater. , 208, 232-242 (1994)

[72]     Z.L. PAN, M.P. Puls, I.G. Ritchie, J. All. and Comp. , 211/212, 245-248 (1994)

[73]     E. Zuzek, Bull. All. Phase Diagrams, 11, 385-395, (1990)

[74]     L.E. ORGAZ-BAQUE, Contribution à l'étude des hydrures des composés intermétalliques et leurs applications dans les pompes à chaleur chimiques, Thèse de l'université Paris-Sud, Centre d'Orsay, (1988)

[75]     P. Dantzer and F. Meunier, Hydrides in Chemical Heat Pumps, Hydrogen Storage Materials, ed : R.G.Barnes, Materials Science Forum, (1988)

[76]     P. DANTZER, M. PONS, A. GUILLOT, Z. Phys. Chem. , 183, 205-212, (1994)

[77]     M. WISE, J. FARR, I. Harris, J. HIRST, Hydrogen in Metals, vol.1, Edition Science et Ind. , Paris (1972)

[78]     R. kronski, t. schober, J. All. and Comp. , 205, 175-178, (1994)

[79]     I. PRIGOGINE, R. DEFAY, Chemical Thermodynamics, Longmans, Green & Co, London, (1954)

[80]     I. PRIGOGINE, Introduction à la thermodynamique des processus irréversibles, Dunod, Paris, (1962)

[81]     W. Mckinnon, J. Less-Comm. Met. , 93, 293, (1993)